【FF】Was ist das Delta einer Option & wie verwendest Du es?

aktualisiert am: September 17, 2023

Autor: TOBIAS SCHMID | Trader / Anleger / Börsenexperte

aktualisiert am: September 17, 2023

Autor: TOBIAS SCHMID | Trader / Anleger / Börsenexperte

Der Preis einer Option wird durch verschiedene Faktoren beeinflusst, die von Optionshändler mit speziellen Kennzahlen, den sogenannten Griechen, beschrieben werden. Das Delta ist der wichtigste und bekannteste unter den Griechen und beschreibt den Einfluss von Kursbewegungen des Underlyings auf den Optionspreis. Alles was Du als Optionshändler zum Delta einer Option wissen musst, erfährst Du in diesem Artikel.

Inhaltsverzeichnis Verbergen

1 Was ist das Delta bei Optionen?

1.1 Delta von Call Optionen und Put Optionen

1.2 Long Delta vs Short Delta

2 Berechnung des Deltas

3 So nutzen Optionshändler das Delta in der Praxis

3.1 Wahl der Strikes bei verschiedenen Optionsstrategien

3.2 Einschätzung der Gewinnwahrscheinlichkeit

3.3 Theorie vs Praxis

3.4 Delta bei Stillhalter-Strategien

3.5 Delta Hedging

4 Delta in Abhängigkeit der Moneyness

4.1 Delta von At The Money Optionen

5 Veränderungen des Deltas bei einer Kursbewegung (Gamma)

6 Delta in Abhängigkeit der Restlaufzeit und von Theta

6.1 Einfluss der Restlaufzeit auf das Delta ist abhängig von der Moneyness

7 Delta in Abhängigkeit der impliziten Volatilität (bzw. von Vega)

8 Delta in Abhängigkeit des Basispreises (Strike) der Option

9 FAQ – Häufige Fragen zum Delta

Was ist das Delta bei Optionen?

Das Delta ist eine Kennzahl für Optionshändler, die zum Ausdruck bringt, wie sich eine Kursbewegung des Underlyings auf den Optionspreis auswirkt. Ein Delta von 0,5 bzw. 50 % bedeutet, dass der Preis der Options sich um 0,50 USD verändert, bei einer Bewegung des Underlyings von einem USD (unter sonst gleichbleibenden Umständen).

Delta von Call Optionen und Put Optionen

Das Delta einer Option kann Werte von -1 bis +1 annehmen. Positive Delta-Werte bedeuten, dass der Optionspreis ansteigt, bei einem Preisanstieg des Underlyings. Call-Optionen haben grundsätzlich ein positives Delta, während Put-Optionen ein negatives Delta haben.

Long Delta vs Short Delta

Beim Kauf einer Call-Option bist Du Long Delta. Das bedeutet, der Optionspreis steigt an, falls der Kurs des Underlyings steigt.

Beim Kauf eines Puts bist Du Short Delta, was bedeutet, dass der Optionspreis ansteigt, wenn das Underlying fällt.

Beim Verkauf einer Call-Option hingegen bist Du Short Delta und Dein Options-Trade erzielt einen Gewinn, wenn das Underlying fällt.

Beim Verkauf einer Put-Option bist Du Long Delta, d.h. Deine Options-Position erzielt einen Gewinn, wenn der Preis des Underlyings steigt.

Key Takeaways

Das Delta ist einer der wichtigsten Optionsgriechen.
Das Delta steht für die Sensivität des Optionspreises gegenüber Kursbewegungen des Underlyings.
Das Delta drückt aus, wie stark sich der Optionspreis verändert, bei einer Kursbewegung des Underlyings um eine Einheit.
Die Berechnung des Deltas erfolgt über Optionspreismodelle, spielt aber in der Praxis keine Rolle.
Das Delta ist zudem eine Schätzung, wie wahrscheinlich es ist, dass eine Option am Verfallstermin In The Money ist.

Berechnung des Deltas

Aus mathematischer Sicht wird das Delta berechnet, indem man die Veränderung des Optionspreises in Bezug auf die Veränderung des Underlying-Kurses betrachtet. Das Delta ist dabei die Steigung der Tangente an die Optionspreiskurve an einem bestimmten Punkt auf der Kurve.

Tafel mit Formeln als Symbol für das Black-Scholes-Modell bzw. für die Black-Scholes-Formel — Das Delta kann mit dem Black-Scholes-Modell berechnet werden. Die Berechnung spielt jedoch in der Praxis des Optionshandels keine Rolle.

Durch den Einsatz von Optionspreismodellen wie dem Black-Scholes-Modell können alle Optionsgriechen (Delta, Gamma, Theta, Vega, Rho) berechnet werden.

Die genaue Funktionsweise der Formel bzw. der Berechnung des Deltas spielt in der Praxis für Optionshändler keine Rolle, da wir das Delta in der Regel einfach in einer Optionskette ablesen können und es nicht selbst berechnen müssen.

So nutzen Optionshändler das Delta in der Praxis

Das Delta spielt für Optionshändler bei fast jedem Trade eine Rolle. Einerseits orientieren sich viele Trader bei der Wahl des Basispreises (Strike) am Delta, andererseits ermöglicht es eine Einschätzung darüber, wie wahrscheinlich es ist, dass die Option am Verfallstermin In The Money oder Out Of The Money ist.

Wahl der Strikes bei verschiedenen Optionsstrategien

Da es eine Vielzahl an Optionsstrategien gibt, mit denen Du die unterschiedlichsten Ziele verfolgen kannst, kann das Delta bei der Wahl der Strikes helfen, um die Wahrscheinlichkeit zu erhöhen, dass das Ziel der Strategie erreicht wird.

Möchtest Du beispielsweise eine Call Option als “Ersatz” für eine Aktie kaufen, ist es wichtig, eine tief im Geld liegende Option mit einem hohen Delta und einer langen Restlaufzeit zu wählen.

Wenn Du hingegen als Optionsverkäufer hauptsächlich vom Zeitwertverfall profitieren möchtest, kann es sinnvoll sein, Optionen mit einem vergleichsweise niedrigen Delta zu wählen.

Wenn Du bspw. einen Iron Condor handelst und das Ziel hast, dass dieser neutral ist (d.h. dass er auf eine Aufwärtsbewegung des Underlyings etwa gleich reagiert wie auf eine Abwärtsbewegung) kannst Du das Delta nutzen und darauf achten, dass Dein Trade Delta-neutral ist.

Wenn Du ein Aktienportfolio mit einem Put absichern möchtest, weil Du von fallenden Kursen ausgehst, kannst Du mit Hilfe des Deltas berechnen, wie hoch Dein “Versicherungsschutz” ist.

So kann Dir das Delta bei jeder Art von Optionsstrategie helfen, um die passenden Strikes auszuwählen.

Sehr wichtig ist: Das Delta ändert sich ständig und ist abhängig vom Einfluss der anderen Optionsgriechen. So ändert sich das Delta zum Beispiel, wenn Zeit vergeht und der Verfallstermin näher rückt oder wenn die implizite Volatilität steigt oder fällt. Natürlich haben auch Kursbewegungen des Underlyings Auswirkungen auf das Delta. (Mehr dazu weiter unten.)

Einschätzung der Gewinnwahrscheinlichkeit

Das Delta wird von Optionshändler auch genutzt, um einzuschätzen, wie wahrscheinlich es ist, dass eine Option am Verfallstermin wertlos (Out Of The Money) oder im Geld verfällt.

Je höher das Delta ist, desto höher ist die Wahrscheinlichkeit, dass die Option im Geld verfällt. Je niedriger das Delta ist, desto geringer ist die Wahrscheinlichkeit, dass die Option im Geld verfällt.

So bedeutet ein Delta von 0,2 bzw. von 20 %, dass die Wahrscheinlichkeit rund 20 % beträgt, dass die Option im Geld verfällt bzw. dass die Wahrscheinlichkeit 80 % beträgt, dass die Option wertlos verfällt.

Theorie vs Praxis

Theoretiker werden hier möglicherweise einwenden, dass das Delta nicht die korrekte Kennzahl ist, um diese Wahrscheinlichkeit zu berechnen. Wenn man streng nach der Black-Scholes-Formel geht, ist tatsächlich das Zeta die korrekte Kennzahl und nicht das Delta, um die Wahrscheinlichkeit zu berechnen, dass die Option im Geld verfällt.

In der Praxis haben sich zudem die Begriffe “Probability Of In The Money” und “Probability Of Profit (POP)” etabliert. In der Trading-Software thinkorswim oder tastytrade zum Beispiel, kannst Du beiden Kennzahlen in der Optionskette anzeigen lassen. Wenn Du die Probability Of In The Money nun mit dem Delta vergleichst, wirst Du feststellen, dass die Unterschiede nur sehr gering sind.

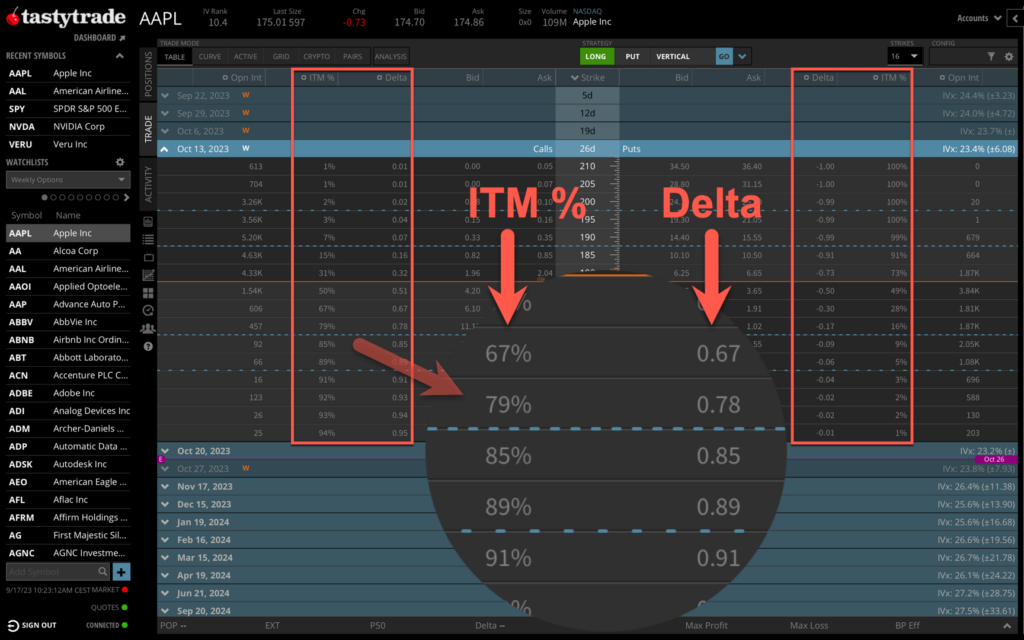
Delta vs ITM % (Wahrscheinlichkeit In The Money) in der Options Chain von tastytrade: Die Werte sind nahezu identisch.

Das bedeutet: In der Praxis ist das Delta allemal gut genug, um die Wahrscheinlichkeit abzuSCHÄTZEN, dass die Option im Geld verfällt. Wir sind schließlich Praktiker. 🙂

Delta bei Stillhalter-Strategien

Stillhalter-Strategien sind auch für private Händler eine der attraktivsten Möglichkeiten, um kontinuierlich Einnahmen durch den Verkauf von Optionen zu generieren. Dabei werden meist Out Of The Money (aus dem Geld liegende) Optionen verkauft.

Wie weit eine Option aus dem Geld liegt, lässt sich mithilfe des Deltas bestimmen. Dabei gilt:

Je geringer das Delta, desto weiter liegt die Option aus dem Geld.

Stillhalter bzw. Optionsverkäufer versuchen meist, Optionen mit einem relativ geringen Delta zu verkaufen. Dies hat einerseits den Vorteil, dass die Gewinnwahrscheinlichkeit bzw. die Wahrscheinlichkeit, dass die Option wertlos verfällt, relativ hoch ist (siehe oben).

Andererseits ist der relative Zeitwertverfall bzw. das relative Theta bei einer weit aus dem Geld liegenden Option mit einem geringen Delta höher. D.h. der absolute Wert, den Du durch den Zeitwertverlust einnimmst (unter sonst gleich bleibenden Umständen) ist bei einer Option mit einem Delta von 20 höher als bei einer Option mit einem Delta von 10. Der prozentuale Wertverlust, bezogen auf den Optionspreis, ist jedoch bei der Option mit dem Delta 10 höher.

Delta Hedging

Delta Hedging ist eine Strategie, die vor allem von Market Makern und institutionellen Anlegern angewendet wird, für private Trader und Anleger jedoch kaum eine Rolle spielt. Wenn in einem Portfolio große Mengen an Optionen verkauft werden, kann das Delta aufsummiert werden, um das Gesamtrisiko zu berechnen. Angenommen es werden 1000 Optionen mit einem Delta von 10 verkauft, so beträgt das Delta:

Delta = 1000 x 0.1 = 100

Das bedeutet, wenn die Aktie zu fallen beginnt, entsteht ein Verlust, der gleichzusetzen ist mit dem Verlust, der entstehen würde, bei einer Long Position von 100 Aktien.

Um dieses Risiko zu hedgen, können nun 100 Aktien leerverkauft werden. Diese gleichen somit den Verlust der Optionen aus. Da sich das Delta bei Kursveränderungen des Underlyings kontinuierlich ändert, muss beim Delta Hedging mit Aktien jedoch kontinuierlich die Anzahl leerverkaufter Aktien angepasst werden. Allein schon wegen der hohen Orderkosten, ist das Delta Hedging für Privatpersonen problematisch. Zudem müssen Positionen kontinuierlich (quasi in Echtzeit) beobachtet und angepasst werden.

Delta in Abhängigkeit der Moneyness

Als Moneyness bezeichnet man die Lage des Basispreises (Strike) einer Option zum aktuellen Marktpreis des Underlyings.

Eine Call Option ist At The Money (am Geld), wenn der Strike auf dem gleichen Kursniveau wie der aktuelle Kurs des Underlyings liegt. Befindet sich der Strike einer Call Option unterhalb des aktuellen Kurses des Underlyings, so ist die Option In The Money (im Geld). Befindet sich der Strike über dem aktuellen Kurs, so ist die Option Out Of The Money (aus dem Geld).

Die Wahrscheinlichkeit, dass eine Option am Verfallstermin einen gewissen Wert (inneren Wert) hat und nicht wertlos verfällt, ist natürlich bei einer tief im Geld liegenden Option deutlich höher, als bei einer weit aus dem Geld liegenden Option.

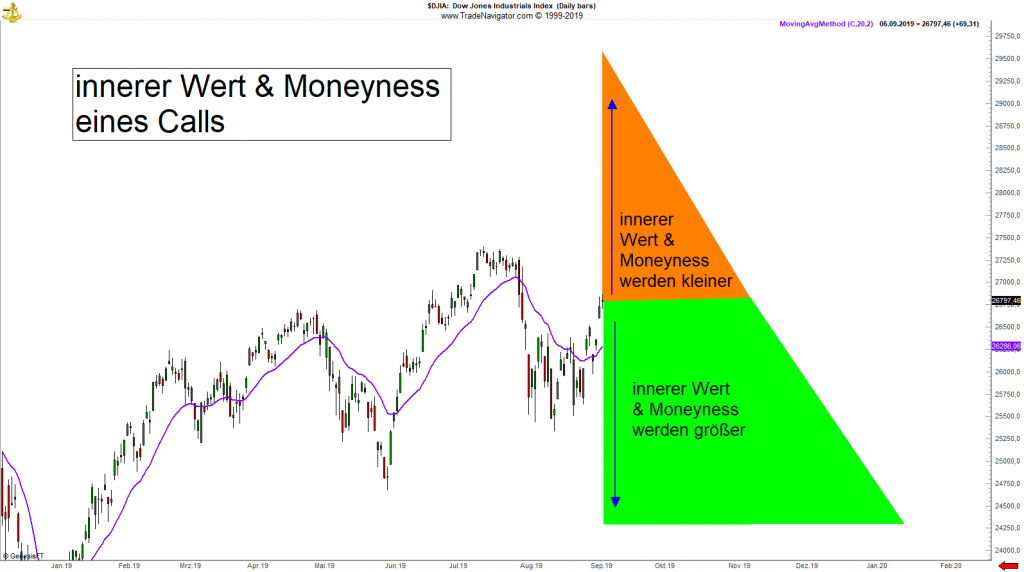
Deshalb ist das Delta einer Option auch desto höher, je tiefer die Option im Geld liegt. Je weiter die Option aus dem Geld liegt, desto geringer ist das Delta.

Eine sehr tief im Geld liegende Option kann ein Delta von fast 100 haben, d.h. der Preis der Option bewegt sich nahezu identisch mit dem Preis des Underlyings und die Wahrscheinlichkeit, dass die Option im Geld verfällt beträgt nahezu 100 %.

Delta von At The Money Optionen

At The Money Optionen haben etwa ein Delta von 50. Hier ist die Ungewissheit also deutlich höher bzw. stehen die Chancen etwa 50/50, dass die Option In The Money oder Out Of The Money verfällt.

Je weiter die Option Out Of The Money liegt, desto geringer ist das Delta.

Selbstverständlich musst Du auch hier beachten, dass sich nach dem Eröffnen eines Trades das Delta bei einer Kursbewegung des Underlyings verändert. Wenn Du bspw. eine Out Of The Money Option mit einem Delta von 14 verkaufst und der Kurs bewegt sich anschließend sehr stark gegen Dich, kann das Delta schnell auf 30 oder 50 ansteigen.

Deshalb ist das Delta auch eine wichtige Kennzahl, mit der Du das Risiko managen kannst. Du kannst bspw. einen bestimmten Delta-Wert als Grenze definieren, bei dem Du den Trade mit Verlust schließen oder die Option Rollen musst.

Veränderungen des Deltas bei einer Kursbewegung (Gamma)

Wie schnell bzw. wie stark sich das Delta bei einer Kursbewegung verändert, verrät Dir die Kennzahl Gamma. Das Gamma gibt an, um wie viele Punkte sich das Delta verändert, bei einer Kursbewegung des Underlyings um eine Einheit.

Wenn Du bspw. eine Out Of The Money Call Option auf eine Aktie mit einem Delta von 15 % bzw. 0,15 kaufst oder verkaufst, bedeutet das zunächst, dass sich der Wert der Option um 0,15 USD verändert, bei einer Kursbewegung der Aktie um einen USD – ceteris paribus, unter sonst gleichbleibenden Bedingungen.

Dieser Wert ist jedoch nur ein theoretischer Wert, da in der Realität die Bedingungen nie gleichbleibend sind. Das Delta verändert sich kontinuierlich. Wenn das Gamma der Option 0,03 beträgt, bedeutet das, dass das Delta von 0,15 (bzw. 15) auf 0,18 (bzw. 18) ansteigt, falls der Kurs der Aktie einen USD ansteigt.

Delta in Abhängigkeit der Restlaufzeit und von Theta

Ein weiterer sehr wichtiger Faktor, der den Preis einer Option und zudem den Wert des Deltas wie auch aller anderen Griechen beeinflusst, ist die Restlaufzeit. Wie genau sich das Delta in Abhängigkeit der Restlaufzeit verändert, ist jedoch davon abhängig, ob es sich um eine Call Option oder um eine Put Option handelt bzw. ob die Option In The Money, At The Money oder Out Of The Money ist.

Einfluss der Restlaufzeit auf das Delta ist abhängig von der Moneyness

Stell Dir vor, eine Aktie notiert aktuell bei 100 USD. Wenn Du eine Call Option mit einem Strike von 120 USD handelst, die eine Restlaufzeit von einem Tag hat, würdest Du sehr wahrscheinlich vermuten, dass die Wahrscheinlichkeit verschwindend gering ist, dass die Option im Geld verfällt und einen inneren Wert erlangt. Dazu müsste der Aktienkurs innerhalb eines Tages um 20 % ansteigen. Deshalb wird das Delta dieser Option 0 oder fast 0 betragen.

Eine In The Money Call Option mit einem Strike von 80 würde mit sehr hoher Wahrscheinlichkeit In The Money verfallen und das Delta würde deshalb nahe bei 100 liegen, da es sehr unwahrscheinlich ist, dass die Aktie innerhalb eines Tages 20 % fällt.

Wenn Du nun Optionen mit den gleichen Strikes (120 bzw. 80) mit einer Restlaufzeit von einem Jahr handelst, ist die Wahrscheinlichkeit schon deutlich höher, dass die Aktie innerhalb eines Jahres auf 120 USD steigt bzw. auf 80 USD fällt. Im Vergleich zu der Option mit einer Restlaufzeit von einem Tag, wird das Delta dieser Out Of The Money Call Option mit dem Strike von 120 wird daher höher sein, das Delta der In The Money Call Option mit dem Strike von 80 wird geringer sein.

Wenn Du eine At The Money Call Option mit einem Strike von 100 USD handelst, die eine Restlaufzeit von einem Tag hat, so beträgt die Wahrscheinlichkeit, dass die Option im Geld verfällt, etwa 50 %. Bei einer Restlaufzeit von einem Jahr beträgt diese Wahrscheinlichkeit ebenfalls rund 50 %. Das bedeutet, dass bei At The Money Optionen die Restlaufzeit keinen bzw. nur einen sehr geringen Einfluss auf das Delta hat.

Key Takeaways

Das Delta von Out Of The Money Optionen wird geringer bzw. tendiert gegen 0, je näher der Verfallstermin rückt.
Das Delta von In The Money Optionen wird größer bzw. tendiert gegen 1 (bei Puts -1), je näher der Verfallstermin rückt.
Eine At The Money Option hat ein Delta von ungefähr 50% und die Restlaufzeit hat nur einen geringen Einfluss.

Delta in Abhängigkeit der impliziten Volatilität (bzw. von Vega)

Neben der Restlaufzeit ist die implizite Volatilität (IV) der wichtigste Einflussfaktor auf das Delta einer Option. Die IV drückt die vom Markt erwartete Schwankungsbreite für ein Underlying aus.

Eine hohe implizite Volatilität bedeutet, dass der Markt eine hohe Schwankungsbreite erwartet. Denken wir nochmal zurück an unser vorheriges Beispiel einer Aktie, die bei 100 USD notiert und einer Call Option mit einem Strike von 120 USD sowie einer Call Option mit einem Strike von 80 USD.

Auch hier ist der Einfluss der impliziten Volatilität abhängig von der Moneyness. Wenn eine hohe Schwankungsbreite erwartet wird, ist es auch wahrscheinlicher (falls die Erwartung korrekt ist), dass einer der beiden Strikes erreicht wird.

Somit gilt:

Je höher die implizite Volatilität ist, desto höher ist das Delta einer Out Of The Money Option (ceteris paribus / unter sonst gleichbleibenden Bedingungen).
Je höher die implizite Volatilität ist, desto geringer ist das Delta einer In The Money Option (ceteris paribus / unter sonst gleichbleibenden Bedingungen).

At The Money Optionen reagieren ebenfalls auf Veränderungen der IV, jedoch nur geringfügig.

Delta in Abhängigkeit des Basispreises (Strike) der Option

Wie oben erwähnt, kann das Delta unter anderem dazu genutzt werden, um abzuschätzen, wie wahrscheinlich es ist, dass eine Option im Geld verfällt.

Daraus folgt:

Je weiter eine Option aus dem Geld ist, desto geringer ist das Delta, da die Wahrscheinlichkeit, dass eine Option im Geld verfällt, desto geringer ist, je weiter der Strike vom aktuellen Kurs des Underlyings entfernt liegt.
Je weiter eine Option im Geld ist, desto höher ist deren Delta.

FAQ – Häufige Fragen zum Delta

Delta ist eine der Optionskennzahlen, auch bekannt als „Griechen“, die verwendet werden, um das Risiko und das Verhalten von Optionen zu bewerten. Delta misst die Sensitivität des Optionspreises gegenüber einer Änderung des zugrunde liegenden Basiswerts (z. B. einer Aktie, eines Index oder eines Futures).

Konkret gibt das Delta an, wie sich der Preis einer Option ändert, wenn der Preis des zugrunde liegenden Basiswerts um eine Einheit (z. B. um 1 Euro oder 1 US-Dollar) steigt oder fällt. Delta kann Werte zwischen -1 und 1 annehmen.

Bei Call-Optionen liegt das Delta in der Regel zwischen 0 und 1, wobei ein Delta von 1 bedeutet, dass der Optionspreis um 1 Euro (oder eine andere Währungseinheit) steigt, wenn der Basiswert um 1 Euro steigt. Bei Put-Optionen liegt Delta zwischen -1 und 0. Ein Delta von -1 bedeutet, dass der Preis der Put-Option um 1 Euro steigt, wenn der Basiswert um 1 Euro fällt.

Das Delta einer Option kann mithilfe von Optionspreismodellen berechnet werden. Eines der bekanntesten Modelle ist das Black-Scholes-Modell, das 1973 von Fischer Black und Myron Scholes entwickelt wurde. Das Black-Scholes-Modell ist ein mathematisches Modell, das den fairen Wert einer Option unter bestimmten Annahmen berechnet. Auf der Grundlage dieses Modells kann das Delta für Call- und Put-Optionen berechnet werden.

Für eine europäische Call-Option lautet die Delta-Formel im Black-Scholes-Modell:

Delta (Call) = N(d1)

Für eine europäische Put-Option lautet die Delta-Formel:

Delta (Put) = N(d1) – 1

Hierbei ist N(d1) die kumulative Verteilungsfunktion der Standardnormalverteilung, die den Anteil der Werte angibt, die kleiner oder gleich d1 sind. Der Parameter d1 ist in beiden Fällen gleich und wird als:

d1 = (ln(S/K) + (r + σ²/2) * T) / (σ * √T)

berechnet, wobei:

S der Preis des zugrunde liegenden Basiswerts ist
K der Ausübungspreis der Option
r der risikofreie Zinssatz
σ die Volatilität des Basiswerts (auch implizite Volatilität genannt)
T die Zeit bis zum Verfall der Option (in Jahren)

Die Berechnung des Deltas kann komplex sein, und es gibt auch andere Optionspreismodelle wie das Binomialmodell oder das Bachelier-Modell, die zur Berechnung des Deltas verwendet werden können. In der Praxis verwenden die meisten Händler und Investoren Software-Tools oder Online-Rechner, um das Delta von Optionen zu berechnen.

Das Delta einer Option wird von verschiedenen Faktoren beeinflusst, die sowohl den zugrunde liegenden Basiswert als auch die spezifischen Eigenschaften der Option betreffen. Die wichtigsten Faktoren, die das Delta einer Option beeinflussen, sind die Moneyness, die Restlaufzeit der Option, die implizite Volatilität sowie indirekt und in eingeschränktem Maß der risikofreie Zinssatz.

Es ist wichtig zu beachten, dass das Delta nicht konstant bleibt, sondern sich im Laufe der Zeit und in Reaktion auf Veränderungen der oben genannten Faktoren ändert. Dieses Phänomen wird als „Delta-Drift“ bezeichnet. Um das Risiko einer Optionsposition effektiv zu steuern, müssen Händler und Investoren das Delta regelmäßig überwachen und gegebenenfalls Anpassungen vornehmen.

Das Delta einer Option zeigt an, wie sich der Preis der Option in Bezug auf eine Änderung des Preises des zugrunde liegenden Basiswerts ändert. Das Vorzeichen des Deltas gibt die Richtung dieser Änderung an.

Positives Delta: Wenn das Delta einer Option positiv ist, bedeutet das, dass der Optionspreis steigt, wenn der Preis des zugrunde liegenden Basiswerts steigt, und fällt, wenn der Preis des Basiswerts fällt. Call-Optionen haben in der Regel ein positives Delta, da der Wert einer Call-Option tendenziell zunimmt, wenn der Basiswertpreis ansteigt. Das Delta für Call-Optionen liegt im Bereich von 0 bis 1.

Negatives Delta: Wenn das Delta einer Option negativ ist, bedeutet das, dass der Optionspreis fällt, wenn der Preis des zugrunde liegenden Basiswerts steigt, und steigt, wenn der Preis des Basiswerts fällt. Put-Optionen haben in der Regel ein negatives Delta, da der Wert einer Put-Option tendenziell zunimmt, wenn der Basiswertpreis fällt. Das Delta für Put-Optionen liegt im Bereich von -1 bis 0.

Wie kann das Delta zur Absicherung von Aktienpositionen (Hedging) verwendet werden?

Das Delta einer Option kann zur Absicherung von Aktienpositionen verwendet werden, indem man Optionen mit gegenläufigem Delta einnimmt. Ziel ist es, das kombinierte Delta der Aktien- und Optionspositionen nahe Null zu halten, wodurch das Preisrisiko des Basiswerts neutralisiert wird. Bei einer Long-Aktienposition kann man beispielsweise Put-Optionen mit einem negativen Delta kaufen, während bei einer Short-Aktienposition Call-Optionen mit einem positiven Delta verwendet werden können. Da sich das Delta im Laufe der Zeit und mit Veränderungen des Basiswertpreises ändert, ist es wichtig, die Absicherungsposition regelmäßig zu überwachen und gegebenenfalls anzupassen.

Delta, Gamma, Theta und Vega sind wichtige Optionskennzahlen, die oft als „Griechen“ bezeichnet werden. Sie messen verschiedene Sensitivitäten des Optionspreises in Bezug auf unterschiedliche Faktoren und spielen eine wichtige Rolle bei der Analyse und Absicherung (Hedging) von Optionspositionen. Hier sind die Unterschiede zwischen diesen Kennzahlen:

Delta: Wie bereits erwähnt, misst das Delta die Sensitivität des Optionspreises in Bezug auf Änderungen des Preises des zugrunde liegenden Basiswertes. Es zeigt, wie viel sich der Optionspreis ändert, wenn sich der Preis des Basiswertes um eine Einheit ändert. Delta liegt im Bereich von 0 bis 1 für Call-Optionen und -1 bis 0 für Put-Optionen.

Gamma: Gamma misst die Sensitivität des Deltas in Bezug auf Änderungen des Preises des zugrunde liegenden Basiswertes. Es zeigt an, wie viel sich das Delta ändert, wenn sich der Preis des Basiswertes um eine Einheit ändert. Gamma ist besonders wichtig für Händler, die ihre Optionspositionen absichern möchten, da es ihnen hilft, das Risiko einer Delta-Änderung zu managen.

Theta: Theta misst die Sensitivität des Optionspreises in Bezug auf die Zeit bis zum Verfall der Option. Es zeigt an, wie viel sich der Optionspreis ändert, wenn ein Tag vergeht. Theta ist in der Regel negativ, da der Zeitwert einer Option im Allgemeinen abnimmt, wenn sich der Verfallstag nähert. Händler, die Optionsstrategien mit dem Ziel einer positiven Theta-Position nutzen, profitieren von der Zeitabnahme des Optionswerts.
Vega: Vega misst die Sensitivität des Optionspreises in Bezug auf die implizite Volatilität des Basiswertes. Es zeigt an, wie viel sich der Optionspreis ändert, wenn sich die implizite Volatilität um einen Prozentpunkt ändert. Vega ist für Händler wichtig, die ihre Positionen gegen Änderungen der erwarteten Volatilität des Basiswertes absichern möchten.

Bewerte diesen Artikel!

Wie hilfreich war dieser Beitrag?

Klicke auf die Sterne um zu bewerten!

Durchschnittliche Bewertung 4.8 / 5. Anzahl Bewertungen: 27

Bisher keine Bewertungen! Sei der Erste, der diesen Beitrag bewertet.

Delta – die wichtigste Kennzahl beim Handel von Optionen